大家今天翻译一篇近期比较受大家欢迎的报告，后续会继续不定期一起学习大佬们的报告。

前言：

目前的监督学习模型是基于 label 作为学习目标，那么是否可以添加经典算法（如排序）来作为约束？

深度学习可以不断优化，很重要的一点是有“反馈”，通过梯度回传不断优化，那么本文的大部分内容在将如何在加入经典算法之后，如何利用数学方法转换，让模型同样拥有“反馈”的能力！！！

文章很长，共一万多字。花了三个晚上才完成，求赞支持一波，谢谢啦

本文是来自 NeurIPS 2021 上的工作介绍，具体的报告视频已上传到 B 站

https://www.bilibili.com/video/BV1sb4y187YV/

下面的内容我也是第一次见到，试着翻译成人话，理解有误的地方还请见谅

论文：https://arxiv.org/pdf/2110.05651.pdf

代码：https://github.com/Felix-Petersen/algovision

标题：Learning with Algorithmic Supervision via Continuous Relaxations

摘要

最近，将算法组件集成到神经体系结构中得到了越来越多的关注，因为它 允许使用新形式的监督（如排序约束或轮廓）来训练神经网络，而不是使用 grouth 真值标签 。该领域的许多方法关注于特定任务的持续放松，并在这方面显示出有希望的结果。但对单个任务的关注也限制了所提出概念在狭窄应用范围内的适用性。在这项工作中，我们基于这些想法提出了一种方法，允许 将算法集成到基于离散条件的一般近似的端到端可训练神经网络结构中。为此，我们在控制结构（如条件语句、循环和索引）中放宽这些条件，以便生成的算法是平滑可微的。为了获得有意义的梯度，通过 logistic 分布对每个相关变量进行扰动，并近似该扰动下的期望值。我们在四个挑战性任务上评估了所提出的连续松弛法模型，并表明它能够跟上为每个单独任务专门设计的放松。

1、简介

人工神经网络已显示出其解决各种问题的能力，从计算机科学中的经典任务（如机器翻译 [1] 和目标检测 [2]）到科学中的许多其他主题（如蛋白质折叠[3]）。同时，存在经典算法，其通常基于给定输入和预定义控制结构（例如排序、最短路径计算等）来解决预定义任务。最近，通过将算法概念集成到神经网络结构中，研究开始将这两个要素结合起来。这些方法允许使用替代监督策略训练神经网络，例如通过可微渲染器学习 3D 表征[4]，[5] 或使用排序信息训练神经网络 [6]，[7]。我们将这些 将算法整合到训练目标中的替代监督策略统一为算法监督：

定义 1（Algorithmic Supervision）

在算法监督中，将算法应用于模型的预测，并监督算法的输出。相反，在直接监督中，模型的预测是直接监督的。这如图 1 所示。

一般来说，为了允许使用集成算法对神经架构进行端到端训练，挑战在于估计各个算法的梯度，例如，通过可微近似。

在这里，大多数解决方案都是针对特定问题定制的，例如，可微排序或渲染。但最近也提出了更通用的框架，用于估计组合优化器的梯度。此类方法的示例包括 Vlastelica 等人 [8] 提出的黑盒组合解算器的微分，以及 Berthat 等人 [9] 提出的通过随机扰动输入来微分优化器。这两种方法都集中于一个问题，即需要估计算法的梯度，以便对包括它在内的神经结构进行端到端的训练。为了解决这个问题，Vlastelica 等人 [8] 通过一步线性化方法估计优化器的梯度，该方法考虑了与优化器输出相关的梯度，从而可以集成任何现成的组合优化器。Berthet 等人 [9] 通过随机噪声干扰离散解算器的输入来估计梯度。

在此背景下，我们 提出了一种使算法可微并估计其梯度的方法 。具体来说，我们 提出了不同算法概念的连续松弛（continuous relaxations），如比较器、条件语句、有界和无界循环以及索引。为此，我们在离散算法中通过 logistic 分布扰动这些变量，我们要计算梯度。这使我们能够估计算法输出采样自由和封闭形式的预期值，例如，与通过蒙特卡罗采样方法（例如[9]）近似分布的方法相比。为了保持计算的可行性，我们通过在条件块序列中合并每个条件块之后的计算路径来近似期望值。对于嵌套的条件块，我们计算准确的期望值，而不合并条件情况。这种折衷允许定期合并路径，从而减少了跟踪所有可能路径组合的需要。当我们在访问变量时对其扰动进行建模时，所有分布都是独立的，这与建模输入扰动的情况形成对比，在这种情况下，所有计算路径都必须单独处理。

为了演示实际方面，我们 将所提出的方法应用于四项任务中，这四项任务利用算法监督来训练神经网络，即排序监督 [6]、[7]、[10]、最短路径监督[8]、[9]、轮廓监督（可微渲染）[4]、[5]、[11]，最后是 Levenshtein 距离监控。虽然前三个设置基于该领域现有的基准，但我们介绍了第四个实验，以展示该思想在可微动态规划领域的新算法任务中的应用。在后者中，来自 EMNIST 数据集[12] 的两个串联字符序列之间的 Levenshtein 距离受到监督，而单个字母保持无监督状态。我们表明，所提出的系统能够在排序监督方面优于当前最先进的方法，而在最短路径监督和轮廓监督方面则具有可比性。

2、相关工作

在下文中，我们将重点关注那些为本工作中考虑的任务提供“放松（relaxations）”的工作。最后，我们回顾了一些关于平滑程序解释的早期工作。

Sorting Supervision

Grover 等人首先提出了用分类监督训练神经网络的任务 [6]。在这种情况下，给出了一组基于串联 MNIST 数字[29] 的四位数，任务是找到从图像到标量的保序映射。这里，CNN 应该为 n 个四位数中的每一个预测一个标量，这样它们的顺序在预测的标量中保持不变。对于训练，仅以输入图像的 grouth 真值顺序的形式给出排序监督，而其绝对值保持无监督。Grover 等人 [6] 通过将置换矩阵放松为双随机矩阵来解决这一问题。Cuturi 等人 [7] 在基准测试中发现了这一点，并通过使用正则化最优传输算法近似排序问题，提出了一种可微指标。

Silhouette Supervision

计算机视觉中的一项工作是三维无监督三维重建的可微渲染器。在这里，最近的方法已经提出了可微渲染器，用于在 13 类 ShapeNet 数据集 [30] 上仅使用二维轮廓监督的三维网格重建 [4]，[5]。Kato 等人[5] 提出了一种渲染器，在该渲染器中，光栅化的代理梯度被近似化，以通过轮廓监控以及 3D 样式转换执行 3D 网格重建。Liu 等人 [4] 通过使用可微聚合过程，提出了一种无代理梯度的可微渲染器，并将其应用于三维网格重建以及姿势 / 形状优化。

Shortest-Path Supervision

Vlastelica 等人 [8] 和 Berthet 等人 [9] 提出的两项工作提出了估算现成优化器梯度的方法。在这种情况下，Vlastelica 等人 [8] 提出了一个最短路径监控实验，在该实验中，针对每种类型的地形，以不同的代价给出地形图像，任务是预测从左上角到相反角的最短路径。将最短路径算法集成到神经结构中，可以使神经网络生成最短路径算法用于预测最短路径的地形的成本嵌入。Vlastelica 等人 [8] 通过发现 Dijkstra 算法的线性化 [31] 来解决这一问题，他们可以对其进行区分。Berthat 等人 [9] 研究了这个问题，通过随机扰动最短路径优化问题的输入，为 Dijkstra 算法生成梯度估计。

Smooth Interpretation

在计算机辅助验证领域的另一项工作中，Chaudhuri 等人 [32]，[33] 提出了一种基于高斯分布随机扰动程序输入的程序平滑方法。这里，通过程序变换传播初始高斯扰动，并通过高斯混合近似扰动输出的最终分布。然后使用无梯度 Nelder-Mead 优化方法对平滑函数进行优化。我们的方法的主要区别在于，我们用逻辑分布扰动所有相关变量（而不是输入），并将其用于基于梯度的优化。

3、方法

为了不断放松算法，从而使其可微，我们放松了所有想要微分的值为 logistic 分布。我们选择 logistic 分布，因为它提供了两个独特的特性，使其特别适合于手头的任务：

（1）logistic 分布比正态分布有更大的尾部，这允许更大的概率质量，因此当两个比较值彼此远离时，有更大的梯度。

（2）logistic 分布的累积密度函数（CDF）是 logistic-sigmoid 函数，可解析计算，其梯度易于计算。这与正态分布的 CDF 形成对比，正态分布没有闭合形式，通常通过多项式近似

具体地说，我们“放松“任何值 x（想要计算梯度的值），是通过添加一个服从 logistic 分布的随机变量方式：

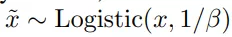
其中 β 是逆温度参数，对于

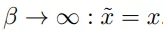
基于此，我们可以放松一个离散条件语句，例如，基于条件 x <c 和常数 c∈ R、详情如下:

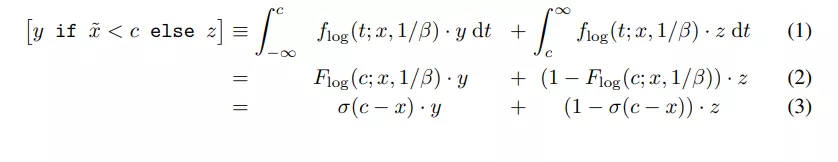
式中，σ 是 logistic(sigmoid)函数 σ（x）=1/（1+e）^−xβ）。在本例中，随着 x 的增加，结果从 y 平滑过渡到 z。因此，结果的导数 wrt。x 定义为：

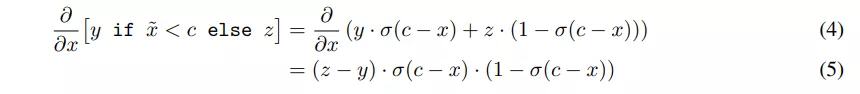
因此，如果 if 案例减少了损失，梯度下降法可以影响条件（˜x<c）保持，或者如果 else 案例减少了损失函数，则影响条件失败。

在本例中，y 和 z 不仅可以是标量值，还可以是算法的结果或算法本身的一部分。这引入了松弛程序流的递归形式，其中算法的部分通过凸组合进行组合：

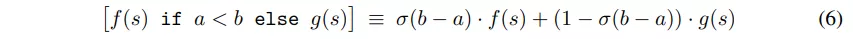
其中，f 和 g 表示函数、算法或语句序列，这些函数、算法或语句通过值调用对所有变量集 s 进行操作，并返回所有变量集 s。此操作的结果可能会覆盖所有变量集（s:=[…]），也可能会在嵌套的条件语句中使用。

在引入上述 if-else 语句之后，我们将这一思想扩展到循环，从而将松弛程序流的形式主义扩展到图灵完整性。在固定循环中，即具有预定义迭代次数的循环中，由于只有一条计算路径，因此不需要松弛，因此，可以通过展开来处理固定循环。

更复杂的情况是条件无界循环，即 While 循环，只要条件成立就执行。为此，让我∈N 是应用 i 乘以循环内容后所有变量的序列。也就是说，对于所有变量 s 的初始集，s0=s，并且 si=f（si−1），其中 f 是循环的内容，即函数、算法或语句序列。设 a，b 分别表示 s 的访问变量，即 s[a]，s[b]。通过递归地应用 if-else 语句的规则，我们获得了无界循环的以下规则：

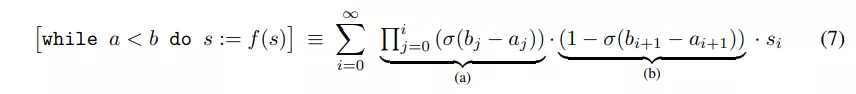
这里，（a）是达到第 i 次迭代的概率，（b）是不超过 i 次迭代的概率。（a）和（b）合在一起是指在应用 i 乘以 f（即 si）之后，有 i 次迭代对所有变量的状态进行加权的概率。在计算上，我们评估无穷级数，直到执行概率（a）在数值上变得可以忽略，或者达到预定义的最大迭代次数。同样，结果可以覆盖所有变量集（s:=[…]），也可以用于嵌套的条件语句中。

Complexity and Merging of Paths

为了计算一个算法在其变量的 logistic 扰动下的精确期望值，必须单独计算所有计算路径，以考虑依赖性。然而，这将导致指数复杂性。因此，我们计算嵌套条件块的精确期望值，但对于连续条件块，我们在每个块的末尾合并计算路径。这使得顺序条件块的数量具有线性复杂性，而只有嵌套条件块的最大深度才具有指数复杂性。请注意，顺序条件块的数量通常远大于条件块的深度，例如，数百或数千个顺序块，最大深度仅为 2− 在我们的实验中。依赖关系的一个例子是表达式 a:=（f（x），如果 i <0，则为 g（x））；b:=（如果 a <0，则为 0；如果 a <0，则为 a2），它包含两个连续条件块之间的依赖关系，这在我们的近似中引入了误差。一般来说，我们的形式主义也支持对顺序条件块之间的依赖关系进行建模，但实际上，对于整个算法来说，它可能变得很难处理。此外，如果算法依赖于特定的依赖关系，则可以明确地考虑相关的依赖关系。

Perturbations of Variables vs. Perturbations of Inputs

注意，变量扰动建模与输入扰动建模不同。差异变得明显的一种情况是，例如，（˜x<x）。在对输入扰动进行建模时，该条件将具有很强的隐式条件依赖性，其计算概率为 0%。然而，在这项工作中，我们没有对输入的扰动进行建模，而是在每次访问变量时对变量的扰动进行建模，以便两次访问一个变量是独立同分布的（iid）。因此，（˜x<x）的概率为 50%。为了最小化松弛的近似误差，仅应松弛需要梯度的变量。

3.1 Relaxed Comparators

到目前为止，我们只考虑了比较器 <. > 通过交换参数进行跟踪

Relaxed Equality

对于相等算子=，我们考虑两个分布 a˜ ∼ Logistic(a, 1/β) 和 b˜ ∼ Logistic(b, 1/β)，我们要检查相似性 / 相等性。给定值 a，我们计算 a 是来自 b˜ 而不是 a˜ 的样本的可能性。如果 a 从 a 和 b 中提取的可能性相等，则 a 和 b 相等。如果 a 不太可能从 b 中提取，则 a 和 b 是不相等的。为了计算 a 从 b˜和 a˜中提取的可能性是否相等，我们取 a 从 b˜中提取的概率（flog（a；b，1/β））和 a 从 a˜中提取的概率（flog（a；a，1/β））之间的比率：

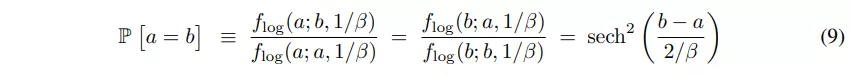
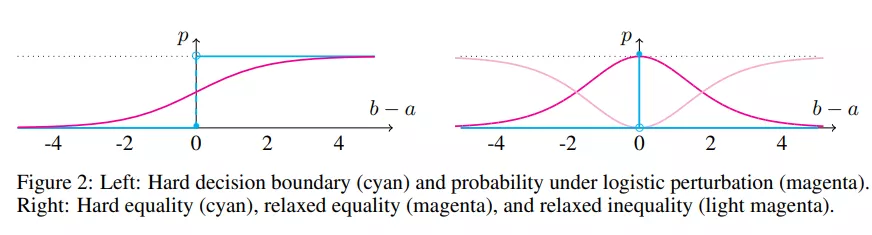
这些松弛比较器如图 2 所示。为了计算合取概率（即 and）或析取概率（即 or），我们分别使用乘积或概率和。这对应于独立事件的交集 / 并集。式 9 的另一种推导是¬（a<b）和¬（a>b）的归一化连接。

Relaxed Maximum

为了比较两个以上的元素并放松 arg max 函数，我们使用多项式 logistic 分布，也称为 softmax 分布。

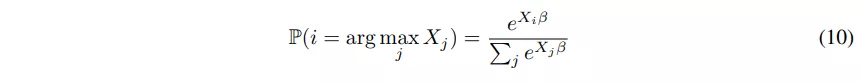
为了放松 max 操作，我们使用 arg max/softmax 的乘积和相应的向量。

Comparing Categorical Variables

比较分类概率分布 X ∈ [0, 1]^n 具有分类概率分布 y，我们考虑两种情况：如果 y∈ {0，1}^n，即 Y 是 one-hot，我们可以使用 X 和 Y 的内积来获得它们的联合概率。然而，如果 Y /∈ {0, 1}^n,，即 Y 不是 one-hot，即使 X = Y 内积也不能是 1，但如果 X =Y，则希望概率为 1。因此，我们（L2）在取内积之前对 X 和 Y 进行归一化，内积对应于余弦相似性。比较分类概率分布的应用示例见第 4.4 节中的 Levenshtein 距离实验。

3.2 Relaxed Indexing

由于向量、数组和张量对于算法和机器学习是必不可少的，我们还将松弛索引形式化。为此，我们介绍了实值索引和分类索引。

Real-Valued Indexing

在松弛算法中，指数可以从实数集合中提取，因为它们可以是计算的凸组合或实值输入。这是一个挑战，因为它需要在多个值之间进行插值。直接方法是网格采样，使用双线性或双三次插值来插值。例如，神经图灵机使用线性插值进行实值索引[35]。然而，在双线性或双三次插值中，超出阵列中直接（或下一个）邻域的关系不建模，也不建模逻辑扰动。因此，我们用 i 值索引 n 维张量 A∈ R n 通过 logistic 扰动，通过应用与 logistic 滤波器 g 的卷积，得到结果为(g ∗ A)(i)。张量 a 与逻辑滤波器 g 的卷积（不要与神经网络中的离散卷积混淆）产生在点 i 处计算的函数 t i ∈ R^n。我们选择 logistic 滤波器而不是双线性和双三次滤波器，因为我们对 logistic 扰动进行建模，另外，因为双线性和双三次滤波器只有紧支撑，而 logistic 滤波器提供无限支撑。这使得建模关系超越了下一个邻居，并且更灵活，因为逆温度 β 可以针对各自的应用进行调整。为了稳定性，我们对用于插值各个索引值的系数进行归一化，使其总和为 1：

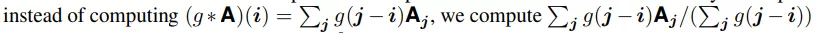
式中，j 是张量 A 的所有有效指数。为了防止优化算法利用混叠效应，我们仅在前向传递中将系数除以其和，但在后向传递（梯度计算）中忽略这一点。实值索引显示在图 3 中，将其与硬索引进行比较

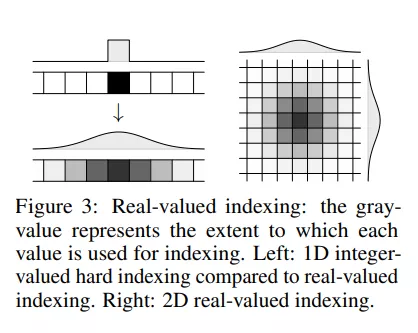
Relaxed Categorical Indexing

如果给出了索引上的分类概率分布，例如，由 argmax 或其松弛 softmax 计算，则可以使用分类索引。这里，边缘分类分布被用作索引张量的权重

请注意，实值索引假设索引数组遵循语义顺序，例如时间序列、图像或网格中的位置。相反，如果数组包含分类信息（如图的节点），则应使用分类索引对值进行索引，因为它们的邻域是任意的。

3.3 Complexity and Runtime Considerations

在运行时间方面，必须注意，运行时间优化算法（例如 Dijkstra）通常不会改善松弛的运行时间，因为对于建议的连续松弛，必须执行算法中的所有情况。因此，减少计算成本的附加条件不会改善运行时，因为两种（所有）情况都会执行。相反，如果一个算法以一个固定的执行顺序来解决一个问题，它将变得非常有益。另一方面，针对运行时优化算法会导致在最快的执行路径之间进行插值。这种优化不能改善梯度，而是降低梯度，因为它是一种额外的近似，并产生与运行时启发式相关的梯度。例如，当放松 Dijkstra 最短路径算法时，在访问节点的不同顺序之间存在插值，这是使 Dijkstra 快速的启发式方法。然而，如果我们必须遵循所有路径（计算松弛度），它可能导致组合爆炸。此外，通过在这些可选顺序之间插值，引入了大量的不确定性，并且梯度也将取决于访问节点的顺序，这两者都是不可取的。此外，执行相当严格的算法可以在 GPU 上并行执行，这样它们可以比 CPU 上运行时优化的顺序算法更快。因此，从运行时和梯度质量的角度来看，我们更喜欢执行结构基本固定且没有运行时优化的简单算法。

4、实验

我们在各种算法监督实验中评估了所提出的方法，其概述如图 4 所示。对于每个实验，我们首先简要描述任务和各自的输入数据以及使用的松弛算法。为了允许应用于各种任务，我们需要为每个算法找到合适的逆温度 β。作为启发，我们从 β =√k，其中 k 是算法中松弛变量的出现次数，这是良好近似和充分松弛之间的平衡，以获得良好的梯度估计。对于每个任务，我们在验证集上调优此参数。所有算法的伪代码以及关于松弛和逆温度参数的附加信息可在补充材料中找到。

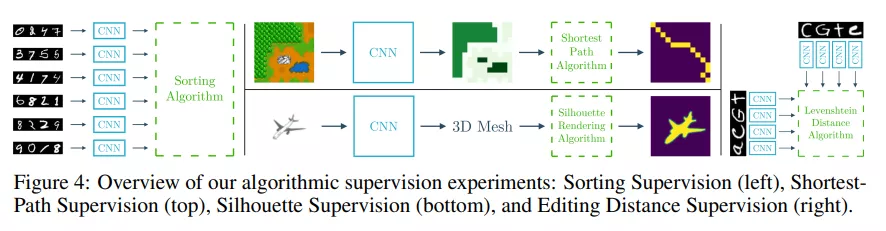
4.1 Sorting Supervision

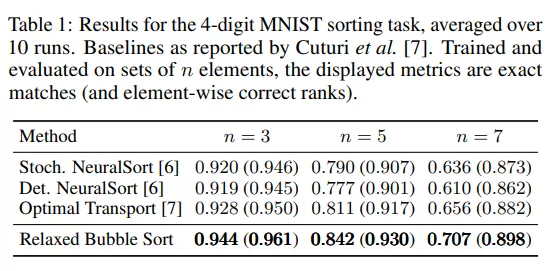
在排序监督实验中，给出了一组基于级联 MNIST 数字 [29] 的四位数字，任务是找到从图像到标量的保序映射 。CNN 学习为 n 个四位数中的每一个预测一个标量，这样它们的顺序在预测的标量中保持不变。为此，仅以输入图像的基本真值顺序的形式提供排序监督，而其绝对值保持无监督。这遵循 Grover 等人[6] 和 Cuturi 等人的协议。

举个例子：

使用我们的方法，我们放松了成熟的稳定排序算法 Bubble sort[37]，该算法通过迭代遍历列表并交换任意两个相邻元素（如果它们的顺序不正确），直到在一次迭代中不再有交换操作为止。我们包含一个变量，如果发生交换操作，通过将输入序列设置为 true 来跟踪输入序列的顺序是否正确。由于松弛，该变量是一个介于 0 和 1 之间的浮点数，对应于预测正确排序的概率（在变量扰动下）。我们用这个概率作为损失函数。该变量等于不需要交换操作的概率，因此 L =1− Q p∈P（1）− p）对于每个潜在交换 p 的概率 p∈ P. 这样，训练目标就变成对输入序列进行排序，因此，神经网络预测的分数对应于监督偏序。事实上，冒泡排序中的交换数对应于肯德尔 τ 系数，它指示序列的排序程度。请注意，例如，快速排序没有此属性，因为即使序列已排序，它也会执行交换。

我们强调，经过训练的神经网络的任务不是对序列进行排序，而是预测每个元素的得分，从而使排序 / 排名与监督排序 / 排名相对应。虽然松弛算法可以正确排序输入，但在评估时，在 [6] 和[7]设置之后，我们使用 argsort 方法测试神经网络产生的输出是否符合基本真值偏序。我们使用与 [6] 和[7]相同的网络体系结构。这里，我们只对 n = 5 的逆温度进行优化，得到 β =8，并对所有其他 n 进行修正。对于培训，我们使用学习率为 10 的 Adam 优化器[38]−4 用于 1.5·105 和 1.5·106 之间的迭代。

我们使用与 Grover 等人 [6] 和 Cuturi 等人 [7] 相同的网络体系结构和评估指标，针对最先进的手工放松排序操作，评估我们的方法。如选项卡中所示。1，我们的一般公式优于 state-of-the-art 的手工放松分拣操作，用于排序监督。

4.2 Shortest-Path Supervision

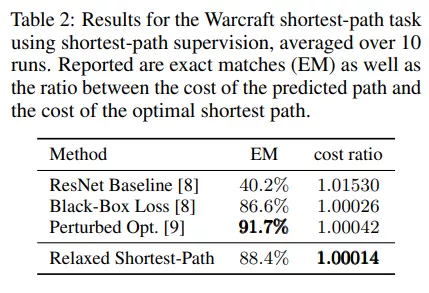
对于 2D 地形上的最短路径监控，我们遵循 Vlastelica 等人 [8] 和 Berthet 等人 [9] 的设置，并使用 10000 块大小为 96×96 的魔兽世界地形（代表大小为 12×12 的地形网格）的数据集。给定地形图像（例如，图 5 第一），目标是根据隐藏成本矩阵（例如，图 5 第三）预测最短路径（例如，图 5 第三）。为此，监督最短路径的 12×12 二元矩阵，而隐代价矩阵仅用于确定最短路径。在他们的工作中，Vlastelica 等人 [8] 和 Berthet 等人 [9] 表明，集成和区分最短路径算法可以通过允许神经网络预测成本矩阵来改进结果，通过该算法可以计算最短路径。这比 ResNet 基线的性能要好得多，在 ResNet 基线中，最短路径只能由神经网络预测（见表 2）。

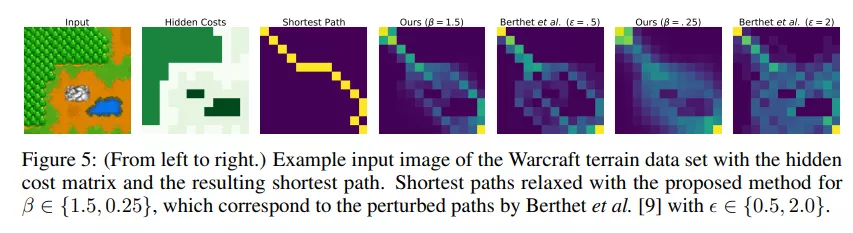
对于这项任务，我们将 Bellman-Ford 算法 [39] 放松为 8 邻域、节点权重和路径重建，补充材料中给出了详细信息。对于监督最短路径和松弛 Bellman-Ford 算法产生的路径之间的损失，我们使用 `2 损失。为了说明通过我们的方法创建的最短路径，并将其与 Berthet 等人 [9] 通过扰动优化器创建的最短路径进行比较，我们在图 5 中显示了两个反向温度的追溯最短路径示例（从中到右）。

我们使用与 Vlastelica 等人 [8] 和 Berthet 等人 [9] 相同的 ResNet 网络体系结构，并且还训练 50 个 epoch，batch 大小为 70。我们使用 β =25 的逆温度。

如选项卡中所示。2，我们的松弛在预测到的最优最短路径的成本比上优于所有基线，并且在最短路径精确匹配精度上达到了仅次于扰动优化器的次优结果

4.3 Silhouette Supervision

从单个二维图像重建三维模型是计算机视觉中的一项重要任务。最近的工作 [4]，[5] 采用可微渲染器，通过反馈重建轮廓是否与输入图像匹配来训练三维重建网络。具体而言，最近的工作已经在 ShapeNet[30]的 13 个对象类的数据集上进行了基准测试 [4]、[5]、[11]，这些对象类是从 24 个方位角以 64×64[5] 的分辨率渲染的。对于轮廓监督学习，单个图像由神经网络处理，神经网络返回 3D 网格。该网格的轮廓由可微渲染器从两个视点渲染，渲染网格和预测网格之间的交集过并用作更新神经网络的训练目标 [4]，[5]。对于训练，我们也使用与 Kato 等人[5] 和 Liu 等人 [4] 相同的神经网络结构。请注意，虽然渲染器可以渲染完整的 RGB 图像，但在这些实验中，只有轮廓用于监督三维几何体重建。具体而言，[4]、[5]的公共实现仅使用轮廓监视。

对于这项任务，我们放松了两种轮廓渲染算法。算法按如下方式栅格化 3D 网格：对于网格的每个像素和每个三角形，如果像素位于三角形内，则输出图像中像素的值设置为 1。像素是否位于三角形内的条件以两种可选方式进行检查：（1）通过三个嵌套的 if 条件检查像素位于每条边的哪一侧。（2）通过检查像素和三角形之间的有向欧几里德距离是否为正。注意，通过使用我们的框架放松这些算法，我们获得了非常接近（1）的 Pix2Vex[40]和（2）的 SoftRas[4]的可微渲染器。图 6 中显示了松弛轮廓渲染的示例和来自数据集的示例图像。

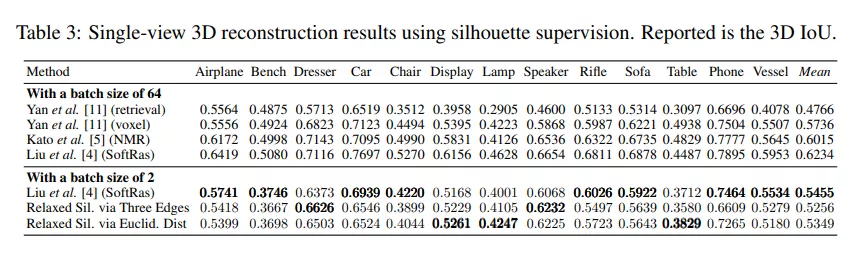
由于简单轮廓渲染器没有任何优化，例如丢弃远离三角形或被其他三角形遮挡的三角形的像素，因此效率不高。因此，由于资源有限，我们只能以 2 的最大批量进行培训，而以前的工作使用 64 的批量。因此，为了进行公平比较，我们仅在 2 个批次上复制了 Liu 等人 [4] 最近表现最好的作品。对于有向欧氏距离，我们使用 β =2000 的逆温度；对于三条边，β=10000。

我们在表 3 中报告平均值和类级 3D IoU 结果。3. 我们的松弛性能优于 Yan 等人 [11] 的检索基线，即使我们使用的批次大小仅为 2。与批量大小为 2 的 SoftRas 渲染器直接比较，我们的松弛实现了 13 个对象类中 5 个的最佳精度。然而，平均而言，我们的方法虽然没有表现出比 SoftRas 更好的性能，但显示出可比的性能，仅下降 1%。值得注意的是，有向欧几里德距离方法的性能优于三边方法。由于计算有向欧几里德距离比三个嵌套 if 子句（即使在宽松的情况下）更昂贵，因此三边方法的速度要快 3 倍

4.4 Levenshtein Distance Supervision

在 Levenshtein 距离监督实验中，我们通过只监督长度为 32 的两个手写字符串之间的编辑距离来监督手写 EMNIST 字母的分类器[12]。作为编辑距离，我们使用 Levenshtein 距离 LD，其定义为：

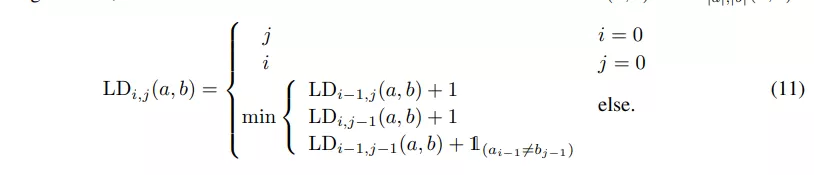
我们使用经典的动态规划算法放松 Levenshtein 距离。图 7 显示了示例 Levenshtein 距离矩阵及其松弛。

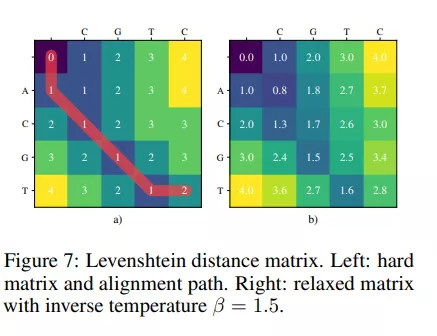
为了便于学习，给出了 32 个手写字符 a、b 的图像串对以及地面真值 Levenshtein 距离 LD（ya、yb）。我们从 2 个或 4 个字符的字母表中抽取一对字符串 a、b。对于给定第一个字符串的第二个字符串的采样，我们统一选择两个或四个插入和删除操作。因此，使用两个不同字符的字符串的平均编辑距离为 4.25，四个字符的平均编辑距离为 5。我们使用 CNN 处理每个字母，CNN 返回字母的分类分布，然后将其反馈给算法。基于 {a，C，G，T} 的一对字符串的示例是 and。我们的培训目标是最大限度地减少预测距离和 grouth 真实距离之间的 l 2 损失：

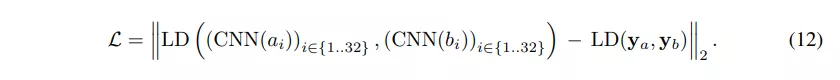
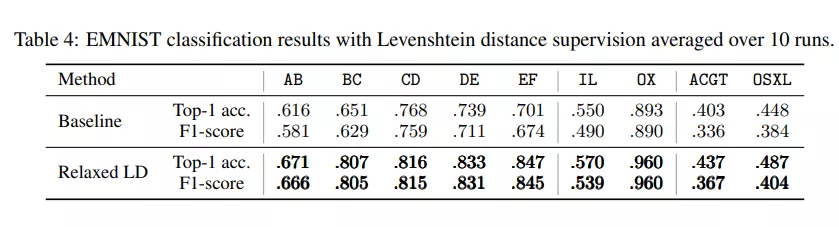
表 4 表明，在所有情况下，我们的方法在这两个指标上都始终优于基线。字符组合 AB、BC、CD、DE 和 EF 是随机组合的标准选择。IL 所代表的字符是两个字母最难的组合，因为它们甚至经常被有监督的神经网络所混淆[12]，人类也无法区分。字符 OX 代表了最简单的情况，因为有监督的分类器可以在测试数据集上完全区分它们[12]。对于两个字母组合，我们在 57%（IL）和 96%（OX）之间实现了顶级精度。即使是四个字母组合（ACGT 和 OSXL），我们也能达到最高 48.7% 的顶级精度。注意，当我们使用长度为 32 的字符串时，在 Levenshtein 算法中，超过 1000 条语句被放松

5、结论

我们提出了一种算法的连续松弛方法，允许将其集成到端到端可训练神经网络结构中。为此，我们使用平滑函数参数化的算法执行路径的凸组合。我们证明了我们提出的通用框架可以在各种算法监督任务上与特定算法的 SOTA 连续松弛以及梯度估计方法竞争。此外，我们证明了我们的公式成功地放松了即使是最短路径算法或渲染器等复杂算法。我们希望激励研究界在我们的框架基础上进一步探索算法监控和算法增强神经网络架构的潜力。

原文链接：https://www.bilibili.com/read/cv13960952/